Introduction to Effective Field Theories in Elementary and Collider
Physics II: Applications
Lecture: University of Vienna, SS 2011
Prerequisits
- Introduction effective field theory course given in the WS 2010/2011
(link to WS 2010/2011 lecture)
- OR -
strong field theory background.
- Standard Model of particle physics
- being comfortable computing Feynman diagrams
Aims
- This is part II of the effective field theory course which concentrates on
specific quantum field theories used in different fields of elementary
particle physics and deepens various concepts of the renormalization
theory.
- Learning how to construct and apply effective field theories.
- Deepen and widen concepts of renormalization and renormalization group
equations..
- See how the theory of quantum fields relates to physical processes.
- Have some fun, ... after all.
Absolutely ESSENTIAL links for particle physicists:
Textbooks
- Heavy Quark Physics, by Aneesh V. Manohar and Mark B. Wise
(Amazon Info)
There is an official list of
errors and misprints. Best book available on Heavy Quark Effective
Theory (HQET).
- Dynamics of the Standard Model, by J. F. Donoghue, E. Golowich, B. R. Holstein,
(Amazon Info)
Excellent text book demonstrating how Standard Model field theory is
applied in particle phenomenology.
- Quantum Field Theory, by Mark Srednicki
(Amazon Info)
Excellent modern field theory book telling you how things are
done. Recommended !
Other useful References
- Many references are from recent scientific literature and given during the course.
- An Introduction to Quantum Field Theory, M. E. Peskin and
D.V. Schroeder (Amazon Info).
There is an official list of errors and misprints.
- Renormalization, by J. Collins (Amazon Info)
- Quantum Field Theory in a Nutshell, A. Zee (Amazon Info)
- Gauge Theory of Elementary Particle Physics, T.-P. Cheng and
L.F. Li (Amazon Info)
- Weak Interactions and Modern Particle Theory, by H. Georgi.
Out of print ... but available here for free!
(You can
make money with this book.)
Be aware of the convention this book uses for γ5.
Lecture
Start: March 4, 2010
Last lecture: June 24, 2011
Friday, 10:15 - 11:45 ( Erwin
Schrödinger Hörsaal, Zi. 3500, physics building)
Office Hours and Infos
Wednesday: 15:30 - 16:30. Send me email in advance.
Mails to students:
Homework Problems
- Interesting and useful homework problems will be identified and mentioned in class
weekly.
- Let me know if you are interested in having a tutorial.
Lecture Notes and Exercises (Click here for the notes and the exercises of part I.)
- Lecture 6:
Composite Operators and
Effektive Weak Hamiltonian
- Exercises (March 8, 2011): Strong Coupling Evolution
(solutions and Mathematica
notebook by Pedro Ruiz-Femenia)
You should carry out the following exercises using Mathematica for some
of the tedious algebra, but not blindly and still employing your brain
for thinking what you are doing. The numerical values for the known
coefficients of the QCD beta-function are as follows:
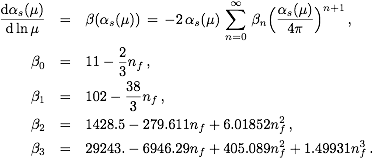 For the numerical evaluations take
nf=5 and αs(MZ)=0.118 for
MZ=91.187 GeV as the initial condition for the solution.
For the numerical evaluations take
nf=5 and αs(MZ)=0.118 for
MZ=91.187 GeV as the initial condition for the solution.
- (1) Strong coupling evolution (numerical): Solve the RGE for the strong
coupling αs. (a) Use the Mathematica routine
NDSolve and program four little routines (or one single one) that
determines αs(μ) from
αs(μ0), μ0 and μ
at one, two, three and four loop order.
- (2) Strong coupling evolution (analytical): There are plenty of
methods for analytic solutions beyond the LL order, because
contributions from higher orders can be treated differently. One
method starts from the relation
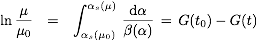 where
where
 and
and
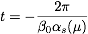 . Determine the coefficients of the
function G(t) and then solve the equation iteratively for
αs(μ). This requires some careful thinking
about what can be expanded in (and what not)
and means that you start with a solution at the LL order level
and determine the higher order contributions in a perturbative
expansion. Note that all logarithmic dependence can be
parametrized conveniently in terms of the expression
. Determine the coefficients of the
function G(t) and then solve the equation iteratively for
αs(μ). This requires some careful thinking
about what can be expanded in (and what not)
and means that you start with a solution at the LL order level
and determine the higher order contributions in a perturbative
expansion. Note that all logarithmic dependence can be
parametrized conveniently in terms of the expression
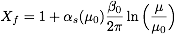 .
You have to keep the two terms in Xf together since they
are both of order one. Plot the relative difference between the
analytic and the purely numerical code at one, two, three and
four loops as a function of μ.
.
You have to keep the two terms in Xf together since they
are both of order one. Plot the relative difference between the
analytic and the purely numerical code at one, two, three and
four loops as a function of μ.
- (3) The hadronic scale &LambdaQCD ("Lambda QCD"): Show that
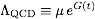 is a RG-invariant quantity.
Analyze the expression at LL order. What is the physical
interpretation of &LambdaQCD? Determine
&LambdaQCD numerically at one, two, three and four
loop order as a function of the renormalization scale μ.
is a RG-invariant quantity.
Analyze the expression at LL order. What is the physical
interpretation of &LambdaQCD? Determine
&LambdaQCD numerically at one, two, three and four
loop order as a function of the renormalization scale μ.
- Exercises (March 15, 2011): Large order behavior of perturbation
theory: Renormalons
(solutions by Maximilian Stahlhofen)
The perturbative series of quantities computed in QCD (and in fact
in essentially all quantum field theories) is not convergent. In QCD one
reason for that is the behavior of quantum corrections related to the
RG-evolution of the strong coupling.
- (1) Large order behavior of the static QCD (Coulomb) potential:
In momentum space the leading order expression for the static QCD
potential between a heavy quark and antiquark has the form
 .
The dependence on the running coupling
αs at the momentum scale accounts for the
summation of the most important higher order logarithmic terms.
Take the running strong QCD coupling αs at LL
order, write the resulting series in powers of
αs(μ) and determine the configuration space
static QCD potential by Fourier transformation,
.
The dependence on the running coupling
αs at the momentum scale accounts for the
summation of the most important higher order logarithmic terms.
Take the running strong QCD coupling αs at LL
order, write the resulting series in powers of
αs(μ) and determine the configuration space
static QCD potential by Fourier transformation,
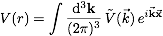 where
where
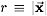 .
.
The result can be determined with relatively little work
using that powers of logarithms
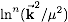 can be generated from derivatives of
can be generated from derivatives of
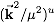 with respective to u.
Rewrite the result in terms of gamma functions only, using the
relation
with respective to u.
Rewrite the result in terms of gamma functions only, using the
relation
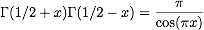 .
Now rewrite the result in term of an exponential with the
logarithm of the Gamma function and use the small u series
expansion of logarithm of the Gamma function
.
Now rewrite the result in term of an exponential with the
logarithm of the Gamma function and use the small u series
expansion of logarithm of the Gamma function
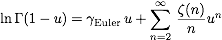 .
Look up the properties of the zeta function ζ(n) for large n
and then determine the asymptotic behavior of the perturbative
coefficients in the &alphas series for the position
space potential in the limit of large order n.
Show that the coefficients diverge with n factorial,
Γ(n+1)=n!.
Series that have such a behavior are said to have a "Renormalon".
.
Look up the properties of the zeta function ζ(n) for large n
and then determine the asymptotic behavior of the perturbative
coefficients in the &alphas series for the position
space potential in the limit of large order n.
Show that the coefficients diverge with n factorial,
Γ(n+1)=n!.
Series that have such a behavior are said to have a "Renormalon".
- (2) Asymptotic series: What does this behaviour mean for the
perturbative series? Do a little survey in the literature (or use
Google) and find the criterion to show that the perturbative
series is in fact an asymptotic series. Discuss during the
tutorial about how such a series can have any physical meaning.
- (3) IR Renormalon: Show that the bad n factorial behavior for
the static configuration space potential at
large orders of perturbation theory arises from small momenta k
in the Fourier integration. The renormalon is therefore called an
infrared-renormalon. One way to solve the exercise is to split the
radial part of the Fourier integral into a low and a large
momentum contribution. This exercise requires from you some over
sight how to use mathematics in an efficient way.
- Exercises (March 23, 2011):
(solutions by Pedro Ruiz-Femenia)
- (1) Muon Decay:
In the Fermi theory the amplitude for muon decay
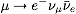 reads
reads
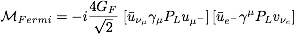 where
where
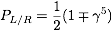 .
Derive the Fermi constant GF within the Standard Model
and determine the muon decay width. You might set the electron
mass to zero. Find the experimental muon width (from the PDG)
and determine GF (with experimental errors).
.
Derive the Fermi constant GF within the Standard Model
and determine the muon decay width. You might set the electron
mass to zero. Find the experimental muon width (from the PDG)
and determine GF (with experimental errors).
- (2) An Alternative Model:
Think back how the SM is constructed and which factors are
relevant for the muon decay. What is the result for the Fermi
constant in a theory in which the left-handed electron and muon
fields are in triplets (with all right-handed fields in singlets)
under
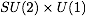 as follows:
as follows:
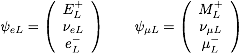 ,
where E+ and M+ are heavy (unobserved)
lepton fields? The SU(2) generators of the triplet
representation are:
,
where E+ and M+ are heavy (unobserved)
lepton fields? The SU(2) generators of the triplet
representation are:
 .
Note that
.
Note that
 .
.
- (3) Neutrino-Electron Elastic Scattering:
In the
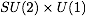 theory, both
W+- and Z0 exchange contribute to the
elastic scattering process
theory, both
W+- and Z0 exchange contribute to the
elastic scattering process
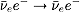 . For momentum transfers very
small compared to MW, show that the amplitude for
this process can be written as
. For momentum transfers very
small compared to MW, show that the amplitude for
this process can be written as
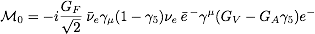 .
Find GV and GA.
.
Find GV and GA.
- Exercises (March 29, 2011):
(solutions by Maximilian Stahlhofen)
- (1) Fierz Transformation:
Find the Cj in the following relations:
 .
These six numbers are all there is to Fierz transformations.
Hint: For (a) and (b), multiply by
γνlk and sum over l and k.
For (c) and (d), it's easiest to avoid taking traces of
&sigmaμν, so multiply by
δlk and sum over l and k to get one equation.
Multiply by &deltajk and sum over j and k to
get another. To prove (b'), multiply by
&gammaλlk and sum over l and k.
.
These six numbers are all there is to Fierz transformations.
Hint: For (a) and (b), multiply by
γνlk and sum over l and k.
For (c) and (d), it's easiest to avoid taking traces of
&sigmaμν, so multiply by
δlk and sum over l and k to get one equation.
Multiply by &deltajk and sum over j and k to
get another. To prove (b'), multiply by
&gammaλlk and sum over l and k.
- (2) Mixing of 4-Quark Operators:
Compute the mixing matrix Zcij of the
operators O1 and O2. Use color and Dirac
Fierz relations discussed in class and recycle results obtained
before for the one-loop renormalization of QED.
- Exercises (April 5, 2011):
(solutions by Maximilian Stahlhofen)
- (1) Semileptonic and Nonleptonic B Decay Rates:
a) Calculate the semileptonic decay rate of a free b quark
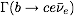 .
Use the effective Hamiltonian discussed in class.
Write down the result for the muon decay rate.
.
Use the effective Hamiltonian discussed in class.
Write down the result for the muon decay rate.
Now Use the effective Hamiltonian discussed in class to
compute the non-leptonic free quark decay rate
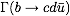 .
Neglect all masses except for the b quark mass.
.
Neglect all masses except for the b quark mass.
- (2) Change of Renormalization Prescription:
The MS
subtraction scheme belongs to the class of ``mass-independent''
renormalization prescriptions. Another such scheme is the
MS subtraction scheme where
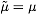 . So, consider the coupling
in some theory
defined in two mass-independent renormalization prescriptions,
λ and
λ.
Their relation can be expressed in terms of a perturbative
series,
. So, consider the coupling
in some theory
defined in two mass-independent renormalization prescriptions,
λ and
λ.
Their relation can be expressed in terms of a perturbative
series,
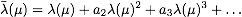 .
Determine the coefficients ai for the couplings
in the MS (λ) and the
The MS
(λ )
schemes for the &phi4-theory.
Prove that the first two coefficients of the β-functions
in both schemes,
.
Determine the coefficients ai for the couplings
in the MS (λ) and the
The MS
(λ )
schemes for the &phi4-theory.
Prove that the first two coefficients of the β-functions
in both schemes,
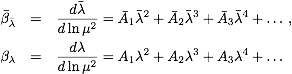 are the same. Do the results also apply to QED and QCD?
are the same. Do the results also apply to QED and QCD?
- (3) Renormalization Group Equations at Higher Order:
a) The renormalization constants of φ4-theory
at two-loop order in the
MS scheme read
 .
Determine the two-loop renormalization group equations.
.
Determine the two-loop renormalization group equations.
Solve the renormalization group equations. To keep the solution
elementary it can be helpful to recall that you anyway need to only
consider the case λ<< 1. Coupling times log, however, is
of order unity.
b) Use the relation between the renormalized and the bare
coupling,
 , to derive the
general expression for
, to derive the
general expression for
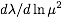 in terms of
Zλ in d=4-2ε dimensions. Use
the fact that
in terms of
Zλ in d=4-2ε dimensions. Use
the fact that 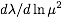 does not diverge for
ε→ 0 to show that the
coefficient of the 1/ε2 term in
Zλ can be determined from
the coefficient of the 1/ε term. For this make the ansatz
does not diverge for
ε→ 0 to show that the
coefficient of the 1/ε2 term in
Zλ can be determined from
the coefficient of the 1/ε term. For this make the ansatz
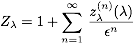 .
and use the fact that zλ(n)
is of order λn, i.e.
.
and use the fact that zλ(n)
is of order λn, i.e.
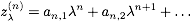 .
Cross-check the result with the two-loop result of
Zλ in φ4-theory.
Explain that in fact all zλ(n)
with n≥2 can be
determined from zλ(1).
Derive the λ3/ε3 and
λ3/&epsilon2 three-loop
contributions of Zλ.
.
Cross-check the result with the two-loop result of
Zλ in φ4-theory.
Explain that in fact all zλ(n)
with n≥2 can be
determined from zλ(1).
Derive the λ3/ε3 and
λ3/&epsilon2 three-loop
contributions of Zλ.
- Exercises (April 10, 2011):
(solutions by Pedro Ruiz-Femenia)
- (1) Non-Leptonic b Quark Decays and Penguin Transitions:
Write down all possible decays of a b quark into
u, d, s and c quarks. (This includes decays into two or three
of the same quarks.) Order the various decay modes into the
following three classes:
- Class I: only current-current operators contribute,
- Class II: current-current and penguin operators contribute,
- Class III: only penguin operators contribute.
Determine the parametric size of the various operators
(take into account matching conditions and CKM factors).
- (2) The decay b → s γ and QCD Equations of Motion:
After integrating out the top, W, Z and Higgs, a number of
local operators are induced which mediate the flavor
changing (electric) charge-neutral process b → sγ.
The operators that are induced include the
local 4-quark operators discussed in class and the following
local 2-quark operators, which we, however, did not discuss
in class:
 Here, Dμ=&partμ +
i g TA AμA +
i e Q Aμ is the covariant derivative
(in the SU(3) fundamental representation) acting
on the quark fields,
(Dμ Gμν)A =
(δAB ∂μ +
g fABCAμ B)
GμνC and
Here, Dμ=&partμ +
i g TA AμA +
i e Q Aμ is the covariant derivative
(in the SU(3) fundamental representation) acting
on the quark fields,
(Dμ Gμν)A =
(δAB ∂μ +
g fABCAμ B)
GμνC and
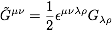 .
.
(a) Write down the combined QCD-QED Lagrangian (i.e.
only operators up to dimension-4) and derive the equations
of motion for the gluon and quark fields. Note that this
is a classic problem. So, for the QED equations of motion
remember your courses on electrodynamics. The QCD equations
of motion are derived in an analogous way.
(b) You can take the classic equations of motion for the
dominant dimension-4 action to reduce the dimension-6
operators shown above to linear combinations of
O8 and O9 and the 4-quark
operators treated in class. One can in fact prove that
this eliminates the 2-quark operators
also at the quantum level. Take ms=0, but
keep the bottom quark mass nonzero. You will find the
identity
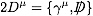 quite useful. For O7 you need the identity
with three gamma matrices
quite useful. For O7 you need the identity
with three gamma matrices
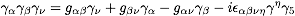 .
.
- Lecture 7:
Heavy Quark Effective Theory
- Exercises (May 3, 2011):
(solutions by Pedro Ruiz-Femenia)
- (1) Heavy antiquarks in HQET:
Recall how the HQET Feynman rules for the heavy quark were
derived in class (propagator and single gluon interaction
vertex). Now consider the corresponding Feynman rules for
the heavy antiquark. Since in HQET the quark and antiquark
dynamics is decoupled (because we do not have to care about
covariance), we want to formulate the effective theory for
heavy antiquarks having positive energy.
In the
 limit, show that the propagator for a heavy
antiquark with momentum pQ = mQ
v+k is
limit, show that the propagator for a heavy
antiquark with momentum pQ = mQ
v+k is
 while the heavy antiquark-gluon vertex is
while the heavy antiquark-gluon vertex is
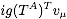 .
This exercise is not difficult, but it requires that you keep
carefully track of color and Dirac indices, and that you know
about charge conjugation and its meaning within the
relativistically covariant formulation of quantum field theory
(Stueckelberg interpretation).
.
This exercise is not difficult, but it requires that you keep
carefully track of color and Dirac indices, and that you know
about charge conjugation and its meaning within the
relativistically covariant formulation of quantum field theory
(Stueckelberg interpretation).
- (2) Operator Renormalizaton in HQET:
Compute the MS
wave function renormaliation constant of a heavy quark.
Now recall the rules to do operator renormalization and
determine the renormalization of the heavy-to-light current
 and the heavy-to-heavy current
and the heavy-to-heavy current
 .
Note that the heavy quark fields in the heavy-to-heavy current
have different v-labels. So while
.
Note that the heavy quark fields in the heavy-to-heavy current
have different v-labels. So while
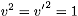 we in general have
we in general have
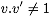 .
Recall that in HQET there are different v-sectors, each
labelled with a different v and that the Feynman rules
in each of these sectors depend on v, but look the same
otherwise. These different v-sectors are coupled through
the heavy-to-heavy currents.
.
Recall that in HQET there are different v-sectors, each
labelled with a different v and that the Feynman rules
in each of these sectors depend on v, but look the same
otherwise. These different v-sectors are coupled through
the heavy-to-heavy currents.
Determine the anomalous dimensions of the heavy-to-light
and the heavy-to-heavy currents. Analyze the anomalous dimension
of the heavy-to-heavy current for the limit
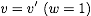 and interpret the result physically.
and interpret the result physically.
- Exercises (May 10, 2011):
(solutions by Maximilian Stahlhofen)
- (1) Anomalous dimension of cF:
Up to order 1/mQ the HQET Lagrangian has the form
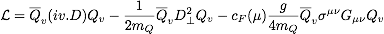 .
Derive the HQET Feynman rules at order 1/mQ
and draw the diagrams one needs to compute to determine the
anomalous dimension of the coefficient cF.
Discuss at the level of the diagrams whether the
1/mQ kinetic energy operator can mix with
the magnetic moment operator. Write down the color
structure of each of the diagrams contributing to the
anomalous dimension of the cF and
argue that the anomalous dimension is proportional to
the QCD color factor CA=3.
(At this point it is helpful to carefully look at the
diagrams and to remember current conservation in QED.)
You don't have to actually compute any of the loop integrals.
.
Derive the HQET Feynman rules at order 1/mQ
and draw the diagrams one needs to compute to determine the
anomalous dimension of the coefficient cF.
Discuss at the level of the diagrams whether the
1/mQ kinetic energy operator can mix with
the magnetic moment operator. Write down the color
structure of each of the diagrams contributing to the
anomalous dimension of the cF and
argue that the anomalous dimension is proportional to
the QCD color factor CA=3.
(At this point it is helpful to carefully look at the
diagrams and to remember current conservation in QED.)
You don't have to actually compute any of the loop integrals.
- (2) Renormalization of HQET at order 1/mQ2:
In the paper hep-ph/9708306 by Bauer and Manohar the LL
renormalization of the HQET Lagrangian up to order
1/mQ2 is carried out. This is actually a
reading assignment which should encourage you to reproduce some
of the results shown in the paper. The only tricky part of the
paper is that it treats the time-ordered products of the
1/mQ operators as individual operators. This is
just a notational trick to formulate insertions of two
1/mQ operators in the framework of a linear (!)
renormalization group equation involving operators at order
1/mQ2.
The Wilson coefficient of such a time-ordered product is
just the product of the Wilson coefficients of the operators
that appear in it. You might actually appreciate how nicely
this simple notational this trick works in practice.
(a) Find the renormalization group equation for cF
and solve it.
(b) Reproduce Eq.(9) which relates the Darwin operator
OD to the operator O1hl
using the gluon equation of motion. This eliminates the
operator O1hl from the anomalous
dimension matrix shown in Eq.(14). Derive the anomalous
dimension matrix for the operator basis where
O1hl is eliminated. Note that in this
paper the anomalous dimension matrix for the operators and
not for the Wilson coefficients is shown!
(c) Find the solution for cD and cF
using the matching conditions
cD(μ=mQ)
=cS(μ=mQ)=1.
- Exercises (May 17, 2011):
(solutions by Pedro Ruiz-Femenia)
- (1) Heavy quark limit and the decays
( D1, D2* )
→ ( D, D* ) + π :
The members of the sl=3/2 (spin of the light degrees
of freedom) doublet ( D1, D2*)
can decay by means of a single pion emission into the two
members of the sl=1/2 ground state doublet
(D, D*). The decay it governed by the strong
interaction. So in addition to parity and angular momentum
conservation, also heavy quark spin symmetry can be applied
in the limit m,sub>c,/sub>→∞. Parity restricts
the orbital angular momentum L of the emitted pion
(P(π)=-1). Determine the relative amplitudes and the relative
decay partial widths for the four possible decays using a
Clebsch-Gordan analysis in the heavy quark limit. You need to
use the Wigner-Eckard theorem and heavy quark spin symmetry to
obtain the expressions for each of the dominant possible
partial waves L. Show among the first things that all
non-zero transitions have a final state with orbital angular
momentum L=2 as the dominant partial wave. Use parity and
angular momentum conservation for the argumentation and
recall that the heavy quark spin is conserved for the deday.
The latter also leads to restrictions of the total spin of the
light degrees of freedome. Only keep the dominant partial wave
for going on.
The largest source of heavy quark symmetry breaking arises
from the fact that the charm mass is actually not really
infinite. This leads to sizeable differences in the phase
spaces available for the pion for the various decay channels.
(Consult the PDG for the D meson and pion masses.)
The phase space of the pion for partial wave L is to a good
approximation proportional to
|pπ|2L+1 in the
(D1, D2*) rest frame,
pπ being the pion momentum. Include the
corrections arising from this effect into the relative size of
the four decay rates and compare to the
experimental numbers in the PDG.
Compare the previous experimental numbers to those for the
analogous decays of the sl=1/2 doublet
(D0*, D1*)
into the ground state doublet plus a pion which have been seen.
Explain the difference. (You only need to compare the overall
size of the rates and shall not carry out the same analysis
you did for the ( D1, D2* )
decays.
- Exercises (May 24, 2011):
(solutions by Maximilian Stahlhofen)
- Non-relativistic Schroedinger Equation :
The non-relativistic Schr\"odinger equation for the positronium
has the form
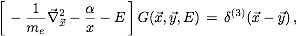 ,
where α is the fine structure constant, me the
electron mass and E the energy of the electron-positron
system with respect to 2me. G is the Green function.
,
where α is the fine structure constant, me the
electron mass and E the energy of the electron-positron
system with respect to 2me. G is the Green function.
(a) Show that
 with β=(E/me)1/2, is a solution
of the Schroedinger equation for
with β=(E/me)1/2, is a solution
of the Schroedinger equation for
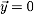 .
.
(b) Compute the integral for G(r,0,E) in terms of
appropriate special functions and determine limit r → 0.
What do the divergences mean? Show that these divergences
lead to infinities in time-independent perturbation theory.
(Consider the corrections caused by the Darwin potential
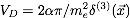 ).
).
(For this exercise you should/must consult function and integral
tables such as Gradstheyn-Ryzhik to find out about the integrals
and the properties of the special functions that result from the
integrals!!!!. The result has the form
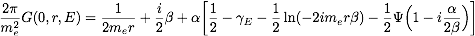 ,
where the Ψ-function is
,
where the Ψ-function is
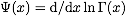 .)
.)
(c) Gr(0,0,E) (or better the expression obtained
in the limit G(r→ 0,0,E)) has poles
at the positronium bound state energies En.
Determine the Coulomb spectrum and the positronium masses
and determine the residue for E → En.
What is the physical meaning of the residue?
(d) Determine the Schroedinger equation for the Green
function in momentum space. Note that
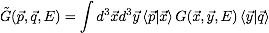 where
where 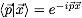 .
.
[The solution has the form
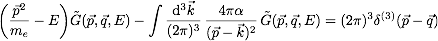 .]
.]
(e) Construct the Green function in momentum space
perturbatively (i.e. iteratively) for small α to
all orders and compute Gdim. reg.(0,0,E) using
dimensional regularization in n=3-2ε
dimension in the limit ε→ 0.
For the two-loop diagram you can use the result
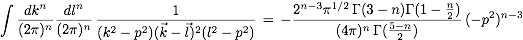 .
For the one-loop diagram you can use the results we already
obtained in previous exercises (see also EFT lecture I).
For the sum of three and more loop diagrams you can use the
expression obtained in (b). (Why?)
.
For the one-loop diagram you can use the results we already
obtained in previous exercises (see also EFT lecture I).
For the sum of three and more loop diagrams you can use the
expression obtained in (b). (Why?)
(f) (Exercise to be demonstrated by the tutor:
Show that one can obtain the integrand of the two-loop
diagram from expanding the electron-positron elastic
scattering amplitude with the exchange of one photon in the
t-channel in the nonrelativistic limit.)
(g) Determine the imaginary part of G(0,0,E) for
positive and negative energies. Show that in the continuum,
for electron-positron scattering with positive energies,
one recovers the famous Sommerfeld factor
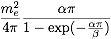 .
Where does this factor play a role? (See e.g. Landau/Lifschitz.)
.
Where does this factor play a role? (See e.g. Landau/Lifschitz.)
Maximal Syllabus (we will not cover all of the items)
- Introductory Part (WS 2010/2011)
- Review of the Standard Model
- Standard Model as part of an effective theory.
- Renormalization and Loops, Part I (WS 2010/2011)
- Decoupling (WS 2010/2011),
- EFT for QED with massive fermions (WS 2010/2011),
- EFT for the Standard Model for heavy top, W, Z
- Unification of gauge couplings (WS 2010/2011)
- Renormalization and Loops, Part II: mixing,
- General Aspects of QCD (WS 2010/2011)
- Behavior of High-Order Perturbation Theory
- Power Corrections
- Renormalons
- Heavy-Quark-Effective Theory
- Symmetries, Action, Power Counting
- Form Factors, CKM Matrix Elements
- Radiative Corrections, Renormalization
- Non-perturbative Corrections
- Inclusive, Semileptonic Decays
- Non-relativistic QCD
- Degrees of Freedom, Action, Velocity Power Counting
- Derivation of the Nonrelativistic Schroedinger Equation
- Lamb-Shift
- Chiral Perturbation Theory
- Chiral Symmetry, Anomalies, Power Counting
- Electromagnetic Processes
- Pion, Kaon Processes
- QCD Factorization, Soft Collinear Effective Theory
- Collinear Fields and Operators, Symmetries, Power Counting
- Factorization
- Deep Inelastic Scattering
- B Decays into light Hadrons
- Aspects of Jet Physics
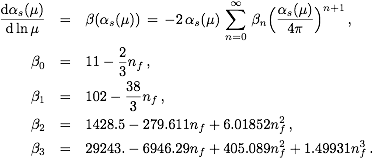
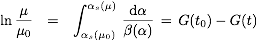 where
where
 and
and
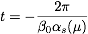 . Determine the coefficients of the
function G(t) and then solve the equation iteratively for
αs(μ). This requires some careful thinking
about what can be expanded in (and what not)
and means that you start with a solution at the LL order level
and determine the higher order contributions in a perturbative
expansion. Note that all logarithmic dependence can be
parametrized conveniently in terms of the expression
. Determine the coefficients of the
function G(t) and then solve the equation iteratively for
αs(μ). This requires some careful thinking
about what can be expanded in (and what not)
and means that you start with a solution at the LL order level
and determine the higher order contributions in a perturbative
expansion. Note that all logarithmic dependence can be
parametrized conveniently in terms of the expression
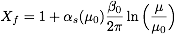 .
You have to keep the two terms in Xf together since they
are both of order one. Plot the relative difference between the
analytic and the purely numerical code at one, two, three and
four loops as a function of μ.
.
You have to keep the two terms in Xf together since they
are both of order one. Plot the relative difference between the
analytic and the purely numerical code at one, two, three and
four loops as a function of μ.
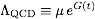 is a RG-invariant quantity.
Analyze the expression at LL order. What is the physical
interpretation of &LambdaQCD? Determine
&LambdaQCD numerically at one, two, three and four
loop order as a function of the renormalization scale μ.
is a RG-invariant quantity.
Analyze the expression at LL order. What is the physical
interpretation of &LambdaQCD? Determine
&LambdaQCD numerically at one, two, three and four
loop order as a function of the renormalization scale μ.
 .
.
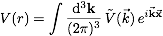 where
where
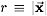 .
.
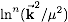 can be generated from derivatives of
can be generated from derivatives of
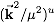 with respective to u.
Rewrite the result in terms of gamma functions only, using the
relation
with respective to u.
Rewrite the result in terms of gamma functions only, using the
relation
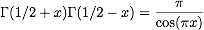 .
Now rewrite the result in term of an exponential with the
logarithm of the Gamma function and use the small u series
expansion of logarithm of the Gamma function
.
Now rewrite the result in term of an exponential with the
logarithm of the Gamma function and use the small u series
expansion of logarithm of the Gamma function
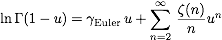 .
Look up the properties of the zeta function ζ(n) for large n
and then determine the asymptotic behavior of the perturbative
coefficients in the &alphas series for the position
space potential in the limit of large order n.
Show that the coefficients diverge with n factorial,
Γ(n+1)=n!.
Series that have such a behavior are said to have a "Renormalon".
.
Look up the properties of the zeta function ζ(n) for large n
and then determine the asymptotic behavior of the perturbative
coefficients in the &alphas series for the position
space potential in the limit of large order n.
Show that the coefficients diverge with n factorial,
Γ(n+1)=n!.
Series that have such a behavior are said to have a "Renormalon".
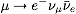 reads
reads
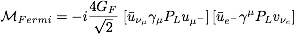 where
where
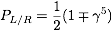 .
Derive the Fermi constant GF within the Standard Model
and determine the muon decay width. You might set the electron
mass to zero. Find the experimental muon width (from the PDG)
and determine GF (with experimental errors).
.
Derive the Fermi constant GF within the Standard Model
and determine the muon decay width. You might set the electron
mass to zero. Find the experimental muon width (from the PDG)
and determine GF (with experimental errors).
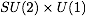 as follows:
as follows:
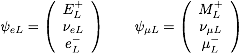 ,
,
 .
.
 .
.
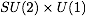 theory, both
W+- and Z0 exchange contribute to the
elastic scattering process
theory, both
W+- and Z0 exchange contribute to the
elastic scattering process
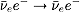 . For momentum transfers very
small compared to MW, show that the amplitude for
this process can be written as
. For momentum transfers very
small compared to MW, show that the amplitude for
this process can be written as
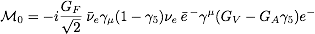 .
Find GV and GA.
.
Find GV and GA.
 .
.
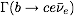 .
Use the effective Hamiltonian discussed in class.
Write down the result for the muon decay rate.
.
Use the effective Hamiltonian discussed in class.
Write down the result for the muon decay rate.
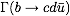 .
Neglect all masses except for the b quark mass.
.
Neglect all masses except for the b quark mass.
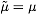 . So, consider the coupling
in some theory
defined in two mass-independent renormalization prescriptions,
λ and
λ.
Their relation can be expressed in terms of a perturbative
series,
. So, consider the coupling
in some theory
defined in two mass-independent renormalization prescriptions,
λ and
λ.
Their relation can be expressed in terms of a perturbative
series,
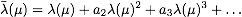 .
.
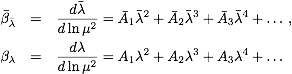
 .
.
 , to derive the
general expression for
, to derive the
general expression for
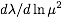 in terms of
Zλ in d=4-2ε dimensions. Use
the fact that
in terms of
Zλ in d=4-2ε dimensions. Use
the fact that 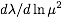 does not diverge for
ε→ 0 to show that the
coefficient of the 1/ε2 term in
Zλ can be determined from
the coefficient of the 1/ε term. For this make the ansatz
does not diverge for
ε→ 0 to show that the
coefficient of the 1/ε2 term in
Zλ can be determined from
the coefficient of the 1/ε term. For this make the ansatz
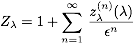 .
.
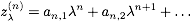 .
Cross-check the result with the two-loop result of
Zλ in φ4-theory.
Explain that in fact all zλ(n)
with n≥2 can be
determined from zλ(1).
Derive the λ3/ε3 and
λ3/&epsilon2 three-loop
contributions of Zλ.
.
Cross-check the result with the two-loop result of
Zλ in φ4-theory.
Explain that in fact all zλ(n)
with n≥2 can be
determined from zλ(1).
Derive the λ3/ε3 and
λ3/&epsilon2 three-loop
contributions of Zλ.

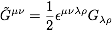 .
.
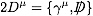 quite useful. For O7 you need the identity
with three gamma matrices
quite useful. For O7 you need the identity
with three gamma matrices
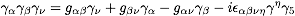 .
.
 limit, show that the propagator for a heavy
antiquark with momentum pQ = mQ
v+k is
limit, show that the propagator for a heavy
antiquark with momentum pQ = mQ
v+k is
 while the heavy antiquark-gluon vertex is
while the heavy antiquark-gluon vertex is
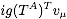 .
This exercise is not difficult, but it requires that you keep
carefully track of color and Dirac indices, and that you know
about charge conjugation and its meaning within the
relativistically covariant formulation of quantum field theory
(Stueckelberg interpretation).
.
This exercise is not difficult, but it requires that you keep
carefully track of color and Dirac indices, and that you know
about charge conjugation and its meaning within the
relativistically covariant formulation of quantum field theory
(Stueckelberg interpretation).
 and the heavy-to-heavy current
and the heavy-to-heavy current
 .
Note that the heavy quark fields in the heavy-to-heavy current
have different v-labels. So while
.
Note that the heavy quark fields in the heavy-to-heavy current
have different v-labels. So while
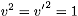 we in general have
we in general have
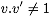 .
Recall that in HQET there are different v-sectors, each
labelled with a different v and that the Feynman rules
in each of these sectors depend on v, but look the same
otherwise. These different v-sectors are coupled through
the heavy-to-heavy currents.
.
Recall that in HQET there are different v-sectors, each
labelled with a different v and that the Feynman rules
in each of these sectors depend on v, but look the same
otherwise. These different v-sectors are coupled through
the heavy-to-heavy currents.
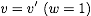 and interpret the result physically.
and interpret the result physically.
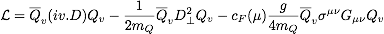 .
.
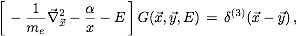 ,
,

 .
.
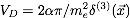 ).
).
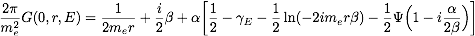 ,
,
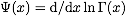 .)
.)
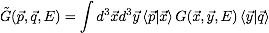
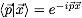 .
.
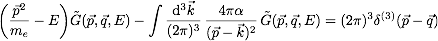 .]
.]
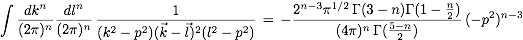 .
.
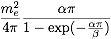 .
.