Introduction to Effective Field Theories in Elementary and Collider Physics
Lecture: University of Vienna, WS 2010/2011
For a link to part II of this course click
here.
Prerequisits
- concepts of quantum field theory
- Standard Model of particle physics
- being comfortable computing Feynman diagrams
Aims
- Learning how to construct and apply effective field theories.
- Deepen and widen concepts of renormalization and renormalization group
equations..
- See how the theory of quantum fields relates to physical processes.
- Have some fun, ... after all.
Absolutely ESSENTIAL links for particle physicists:
Textbooks
- Heavy Quark Physics, by Aneesh V. Manohar and Mark B. Wise
(Amazon Info)
There is an official list of
errors and misprints. Best book available on Heavy Quark Effective
Theory (HQET).
- Dynamics of the Standard Model, by J. F. Donoghue, E. Golowich, B. R. Holstein,
(Amazon Info)
Excellent text book demonstrating how Standard Model field theory is
applied in particle phenomenology.
- Quantum Field Theory, by Mark Srednicki
(Amazon Info)
Excellent modern field theory book telling you how things are
done. Recommended !
Other useful References
- Many references are from recent scientific literature and given during the course.
- An Introduction to Quantum Field Theory, M. E. Peskin and
D.V. Schroeder (Amazon Info).
There is an official list of errors and misprints.
- Renormalization, by J. Collins (Amazon Info)
- Quantum Field Theory in a Nutshell, A. Zee (Amazon Info)
- Gauge Theory of Elementary Particle Physics, T.-P. Cheng and
L.F. Li (Amazon Info)
- Weak Interactions and Modern Particle Theory, by H. Georgi.
Out of print ... but available here for free!
(You can
make money with this book.)
Be aware of the convention this book uses for γ5.
Lecture
Start: October 8, 2010
Last lecture: January 28, 2011
Friday, 10:15 - 11:45 ( Erwin
Schrödinger Hörsaal, Zi. 3500, physics building)
Office Hours and Infos
Wednesday: 16:00 - 17:00. Send me email in advance.
Mails to students:
Oct. 8 ,
Oct. 14 ,
Oct. 19 ,
Oct. 23 ,
Oct. 30 ,
Nov. 3 ,
Nov. 8 ,
Nov. 16 ,
Nov. 21 ,
Nov. 30 ,
Dec. 7 ,
Dec. 14 ,
Jan. 9 ,
Jan. 14 ,
Jan. 24 ,
Feb. 1
Homework Problems
- Interesting and useful homework problems will be identified and mentioned in class
weekly.
- Let me know if you are interested in having a tutorial.
Lecture Notes and Exercises
- Intro Lecture: Concepts of effective theories
- Lecture 1: Introduction
to quantum chromo dynamics (QCD)
- Lecture 2: Basics of the QCD Lagrangian
- Lecture 3: FeynmanRules
- Exercises (October 29, 2010): (solutions by Pedro Ruiz-Femenia)
- (1) Rederive for yourself the various computations in deriving x-space
Green functions in phi^4 theory as discussed in class and go to
second order in lambda for the connected 2-point Green
function. This gives you all relevant two-loop
diagrams. Try to be efficient handling the computations !!! They
can be short and efficient or tedious and time consuming.
- (2) Determine the momentum (Fourier) space 2-loop Green function as defined in
class, i.e. using the convention of incoming external
momenta. You should already use the contraint that the external
momenta satisfy energy-momentum conservation, so not all external moments are
independent. (For the mom-space connected Green function you can
neglect the overal factor (2Pi)^4 times delta-function.)
- (3) Look at the results and set up rules how to get to the results
without considering first the x-space
computations. Are the symmetry fators modified when
switching from position to momentum space?
- (4) Apply the rules of (3) to determine the Feynman diagrams of the connected 4-point
function up to O(lambda^2) and determine the expressions for the
diagrams im momentum space. If you have trouble
determining the symmetry factors go through (1) to
determine them explicitly. Then try to understand
the rules for the symmetry factors you could not determine.
- Exercises (November 5, 2010): (solutions by Maximilian Stahlhofen)
- (1) Derive the Feynman rules (vertex factors and propagators) of QED
in R_xi gauge. For the functional derivative
w.r. to the electron fields (which are Grassmann quantities) you
should use the convention that derivative of the barred electron
fields always stands to the right, i.e. they act first. The
solutions is already given in the notes.
- (2) Derive the Feynman rules (vertex factors and propagators) of QCD
in R_xi and in axial gauge.
- Exercises (November 12, 2010): (solutions by Pedro Ruiz-Femenia)
- (1) Consider the generic generating functional
W[α,α]
for a single fermion theory with a generic fermion current source
LI =
ψ(x)
V(x) ψ(x) which was discussed in the class. V(x) represents
bosonic structures.
(a) Compute the connected 4-point Green function
<0| ψ(x1) ψ(x2)
ψ(x3)
ψ(x4)
|0> at tree level.
The two diagrams you obtain have a relativ minus sign. Look back
how this sign is generated and formulate the corresponding
rule.
(b) Consider that V(x) represents an external source for the
fermion current, i.e. you can consider it another bosonic particle
that interacts with the fermions. Compute the Green function for a fermion
loop generated from n such sources at x1, ..., xn.
- (2) The physics content of a field theory is unchanged by
field redefinitions. Consider the free part of the Lagrangian of
the φ4 field theory and make the field redefinition
φ → φ+ λφ2.
Work out the Feynman rules of the field-redefined theory and
determine the scattering amplitude for
φφ → φφ at tree level. Show that the
amplitude is zero. This is because you are still having a free
field theory in disguise.
- Lecture 4:
Loops and Renormalization
- Exercises (November 19, 2010): (solutions by Maximilian Stahlhofen)
- (1) Compute
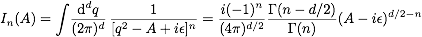 in d=4-2ε dimensions, where A is a real number. We assume
that there are one time and d-1 spatial dimensions. You
are supposed to do the computation in two different ways. Use
Mathematica or tables when needed.
in d=4-2ε dimensions, where A is a real number. We assume
that there are one time and d-1 spatial dimensions. You
are supposed to do the computation in two different ways. Use
Mathematica or tables when needed.
(a) First show that the total solid angle in n dimensions has
the form
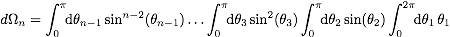 and has the result
and has the result
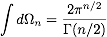 .
.
(b) The first way is to use the Wick rotation in order to turn
the d-Minkowski integral into an Euklidean integration.
(c) The second way avoids Wick rotation. Do the q0 integration by
residues and then carry out the d-1 dimensional spatial
integral afterwards.
- (2) Dimensional regularization regularizes UV as well as IR
divergences. Sometimes both kinds appear in the same loop
diagram, and it is necessary to distinguish them.
Consider the scaleless integral
 .
Convince yourself that it is UV and IR divergent for
d=4. Idenfify the UV-divergence by making the massless
propagators massive,
q2+iε→
q2-m2+iε. Determine the form of the
IR divergence for ε→ 0. Use Mathematica to expand
the d-dimensional result for small ε.
.
Convince yourself that it is UV and IR divergent for
d=4. Idenfify the UV-divergence by making the massless
propagators massive,
q2+iε→
q2-m2+iε. Determine the form of the
IR divergence for ε→ 0. Use Mathematica to expand
the d-dimensional result for small ε.
- (3) Use Mathematica or tables to show the Feynman parameter relations
 and
and
 .
The first relation is used when A and B have the same mass
dimensions and x is dimensionless. The second relation is used
then A and B have different dimensions, and [λ]=[B]-[A].
.
The first relation is used when A and B have the same mass
dimensions and x is dimensionless. The second relation is used
then A and B have different dimensions, and [λ]=[B]-[A].
- (4) Compute the integral
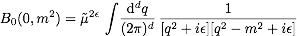 in
two ways. (The term
in
two ways. (The term
 is just a constant.)
is just a constant.)
(a) Use Wick rotation to turn the integral into a Euklidean
integral such that you can then do the radial integration
using Mathematica or tables.
(b) Use the first Feynman parameter relation to turn the
integral into a form to use In from exercise (1).
Use Mathematica or tables for the remaining Feynman parameter
integral over x.
- Exercises (November 26, 2010): (solutions by Pedro Ruiz-Femenia)
- (1) Compute the contraction of gamma matrices
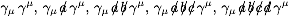 and
the traces
and
the traces
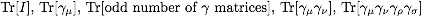 in
4 and d dimensions.
in
4 and d dimensions.
- (2) Derive the renormalized QED Lagrangian to one-loop order using
the multiplicative renormalization relations
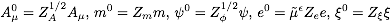 between bare and renormalized fields, mass and coupling. Use that
to one-loop order one can expand the renormalization constants as
between bare and renormalized fields, mass and coupling. Use that
to one-loop order one can expand the renormalization constants as
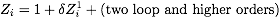 .
.
- (3) Derive the Feynman rules of renormalized QED and write down the
complete set of vertex functions (one-particle irreducible,
amputated Green functions) to one-loop order. This amounts to the
fermion and photon 2-point functions and the fermion-photon
vertex. Write down the corresponding loop integrals and carry out
gamma matrix contractions and traces in d dimensions.
- Exercises (December 3, 2010): (solutions by Maximilian Stahlhofen)
- (1) Compute the integral
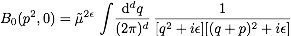 that was
used in class for the renormalization of the photon 2-point function.
that was
used in class for the renormalization of the photon 2-point function.
- (2) Carry out the tensor reduction computations carried out in class for
the one-loop integrals
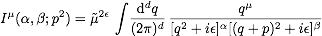 and
and
 .
.
- (3) Determine the one-loop MS
counter terms for φ4-theory with
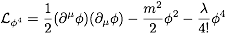 .
Proceed as was done in class for QED.
In this exercise you need to apply most of what you have learned
before. Do the simplest possible computations to get the results
particularly for the 4-point functions. The results are relevant
for the Higgs sector of the Standard Model.
.
Proceed as was done in class for QED.
In this exercise you need to apply most of what you have learned
before. Do the simplest possible computations to get the results
particularly for the 4-point functions. The results are relevant
for the Higgs sector of the Standard Model.
- Exercises (December 10, 2010): (solutions by Pedro Ruiz Femenia)
- (1) Determine the MS
leading logarithmic (one-loop) renormalization group equations of
φ4-theory using the renormalization constant
determined last week and compute their solutions as shown in class.
- (2) The renormalization group equations remain valid even if
m2 is negative and φ get a vacuum expectation
value. Set
 and
compute the vacuum expectation value v. Show that the scalar field
has the mass
and
compute the vacuum expectation value v. Show that the scalar field
has the mass
 .
Now assume that φ4-theory is a model for the
Standard Model Higgs. This model is actually quite accurate in
many respects.
We know that
.
Now assume that φ4-theory is a model for the
Standard Model Higgs. This model is actually quite accurate in
many respects.
We know that
 and
can use the MS
and
can use the MS
 in the Higgs mass expression.
Determine the renormalization scale μ where the Higgs self
coupling diverges and the theory for sure breaks down as a
function of the Higgs mass. Which field theoretic and physical
conclusions do you have to draw? Why - in this light - is LHC a
no-loose experiment?
in the Higgs mass expression.
Determine the renormalization scale μ where the Higgs self
coupling diverges and the theory for sure breaks down as a
function of the Higgs mass. Which field theoretic and physical
conclusions do you have to draw? Why - in this light - is LHC a
no-loose experiment?
- (3) Take the ansatz
 for the QED coupling renormalization constant and determine the
two-loop renormalization group equation pushing the computation
we did in class to one higher order. Show that, if the
renormalization group equation is finite for
for the QED coupling renormalization constant and determine the
two-loop renormalization group equation pushing the computation
we did in class to one higher order. Show that, if the
renormalization group equation is finite for
 ,
b is not independent but a function of a. Determine the function.
,
b is not independent but a function of a. Determine the function.
- Exercises (January 9, 2011): Asymptotic Expansion and Powercounting (solutions by Maximilian Stahlhofen)
Consider the following one-dimensional integral
 .
You can think of this integral as being a simplified version of a loop-Feynman
diagram where the denominator corresponds to a propagator structure. The
concepts discussed in this exercise apply to usual Feynman diagrams as well.
It is your task to compute the expansion for small a<<1. Naive expansion
in a before integration does not work because of an IR singularity.
You might want to compute the integral exactly and then expand the result
for small a, but this is very difficult. Instead use the two methods
below. Use Mathematica for the computations so same some work.
.
You can think of this integral as being a simplified version of a loop-Feynman
diagram where the denominator corresponds to a propagator structure. The
concepts discussed in this exercise apply to usual Feynman diagrams as well.
It is your task to compute the expansion for small a<<1. Naive expansion
in a before integration does not work because of an IR singularity.
You might want to compute the integral exactly and then expand the result
for small a, but this is very difficult. Instead use the two methods
below. Use Mathematica for the computations so same some work.
- (1) Cutoff Method:
In the limit a « 1 the integral is governed by the two
regions k<<1 ("hard") and k &sim a << 1 ("soft"). That's
the reason why naive expansion does not work. Separate the soft
and the hard regions by introducing a cutoff &Lambda with
a << &Lambda << 1 which splits the integral into two parts,
|k|< &Lambda and |k|> &Lambda. Carry out the Taylor expansions
that now become possible in the two regions and do the
integrations. Expand the individual results of the integration
using that a<< &Lambda << 1 and add back together the results.
In this way determine the expansion of f(a) neglecting term at
order a2 or higher. Check your result numerically with
Mathematica.
Since &Lambda has been introduced by hand the
result should be independent of it at any order in the
a expansions. Which problem emerges?
- (2) Dimensional Regularization:
You can use dim reg to do a similar computation. While the cutoff
method is probably quite intuitive and easy to understand for
you, using dim reg involves a number of subtle issues you have to
get used to, but it is more powerful in practice.
So, first continue the integral to
D=1-2&epsilon,
 .
where
.
where
 is the D-dimensional
angular integral and
is the D-dimensional
angular integral and
 .
.
Expand the integrand for the soft regime (a,k<<1) as
described in (1), integrate the terms in
D dimensions and
expand for &epsilon &rarr 0. Remember what you have learned in
class about doing integrations in dim reg.
Have a look at the terms you obtained in the expansion for
small k before integration and observe the order in a they
contribute. Establish so-called power counting rules for the soft
regime that tell you (before integration!) to which order each
term contributes. Determine all terms up to (including) order a.
Expand the integrand for the hard regime (k &sim 1) as described
(1), carry out the integral in
D dimensions and
expand for &epsilon &rarr 0. Establish the power counting rules
in the hard regime and determine all terms up to (including)
order a.
Now add the contributions you got from the expansions in the
soft and the hard regime. The result is the expansion of f(a)
for small a and should agree with your result from (1).
(If you are motivated, compute also the order a2
terms.) Think about how this could have all worked out.
Which way of computing the expansion do you find more
attractive?
- Lecture 5:
Decoupling, Integration out Heavy Particles and Basics of Constructing Effektive Theories
- Exercises (January 14, 2011): Matching with Massive Electrons (solutions by Pedro Ruiz-Femenia)
Consider the standard QED describing the dynamics of electrons and
photons. As discussed in class, for photon momenta
qμ much smaller than me one can integrate
out the electrons and work with a low-energy effective theory
containing only the photons. This effective theory is called the
Euler-Heisenberg theory.
- (a) Determine the one-loop photon vacuum polarization diagram with
dimensional regularization as discussed in class in the
MS renormalization
scheme and expand it for small q2/me2.
Explain why the first term in the expansion motivates matching
onto the effective theory at the scale μ of order me
rather than, let's say, at μ of 100 TeV. The usual convention
is to match at μ=me.
- (b) Take the dimension-6 photonic operator in the effective theory
discussed in class and show that its Feynman rule can reproduce
the momentum-dependence of the second term in the expansion of
the one-loop vacuum polarization function. Fix the Wilson
coefficient c1(μ=me) of the dimension-6
operator such that it reproduces the second term exactly.
Determine the Wilson coefficients of the effective theory up to
dimension-6 (c0, c1) for matching at a
scale μ≠ me.
- (c) You need to check whether what you did is unambiguous by
showing that there is no other photonic dimension-6 operator
that is gauge-invariant and might do the same job. Write down
a few other possibilities and use integration by parts and the
equation of motion in the effective theory
∂μFμν=0 to show that other
possibilities either vanish or reduce to the one you already
used in part (b).
- (d) Look up how the electron and photon fields transform under
C, P and T and show that QED is C-,P- and T-invariant.
Show why these symmetries forbid dimension-6 operators with
three field strengths from ever appearing. (This feature is
also known as ``Furry's Theorem''.)
- (e) At dimension-8, operators are generated which describe
light-by-light scattering (γγ→γγ).
Write down QED one-loop diagrams that can match onto these
operators and determine the power of α contained in
their Wilson coefficients. Use this information and simple
dimensional analysis in the effective theory (e.g. take all
numbers that arise of order one, but keep momenta, masses
and couplings) to obtain a numerical estimate for the cross
section γγ→γγ for 10 keV
photons. Does the reaction happen at a large rate?
Compare to QED cross sections you might have computed
before in other lectures.
- Exercises (January 24, 2011): Gauge Coupling Unification in a (SUSY)
SU(5) GUT
(solutions,
dynamic
Mathematica notebook showing the effects of SUSY particles
(you need to evaluate all definitions to view the dynamic plot),
by Maximilian Stahlhofen)
We discussed SU(5) gauge coupling unification in class. Assuming a
SU(5) gauge symmetry exists at very high energy scales with a
gauge coupling gGUT one can argue that the symmetry is
broken (e.g. by some Higgs mechanism) down to
SU(3)×SU(2)×U(1) at some scale μ=MGUT. If
MGUT is very much larger than the electroweak scale,
one should integrate out all the heavy fields and switch to an
effective theory that has the symmetries
SU(3)×SU(2)×U(1). (Since this is all a model, one can
just assume that all the heavy particles have similar mass of
order MGUT.) When doing the matching computations at
the GUT scale one finds that the breaking patten requires that the
gauge couplings for the unbroken symmetries, gs,
g2, g1 are functions of the original gauge
couplings,
gs=gGUT,
g2=gGUT,
g1=√(3/5) gGUT.
(where s=SU(3),2=SU(2),1=U(1)). One can test whether this
unification idea is consistent with low energy data using the
measured results for the $\overline{\rm MS}$ couplings obtained from
experiments at LEP (μ=MZ=91.2 GeV),
sin2(θW)(MZ)=0.232,
α(MZ)=(128.9)-1,
&alphas(MZ)=0.118± 0.003.
The error in the electromagnetic coupling and the Weinberg angle
is at the level of 0.1%.
- (a) Assume that the effective low energy theory below MGUT
is the Standard Model. Determine the values for the
MS $MS} couplings
αs=(gs)2/(4π),
α2=(g2)2/(4π) and
α1=5(g1)2/(12π) at the
scale MZ. The LL RGE's for these
couplings have the form
 with b1=-2/3nf-1/10nh,
b2=22/3-2/3nf-1/6nh,
b3=11-2/3nf, where nf is the
number of quarks and nh the number of Higgs doublets.
(You can treat the top quark as a light quark in this
context. Think about why this is still a valid approximation
in this case.) Compute the LL solution for the running couplings
above MZ taking the values at MZ as an
input. Is the SU(5) unification scenario consistent with low
energy data?
with b1=-2/3nf-1/10nh,
b2=22/3-2/3nf-1/6nh,
b3=11-2/3nf, where nf is the
number of quarks and nh the number of Higgs doublets.
(You can treat the top quark as a light quark in this
context. Think about why this is still a valid approximation
in this case.) Compute the LL solution for the running couplings
above MZ taking the values at MZ as an
input. Is the SU(5) unification scenario consistent with low
energy data?
- (b) Assume that the effective theory below MGUT is not
the Standard Model, but the minimal supersymmetric Standard
Model (MSSM). Since no supersymmetric (SUSY) partner of any
Standard Model has ever been seen, this scenario is only
possible if all SUSY partners are much heavier than any of
the Standard Model particles. Let us assume that all SUSY
partners have similar masses of order $MSUSY.
So for scales below $MSUSY one can integrate
out the SUSY partners finally arriving at the Standard Model as
the effective theory for scales below MSUSY.
The matching conditions for the gauge couplings at
μ=MSUSY are just as discussed in class.
The MSSM anomalous dimensions have the form
b1=-nf-3/10nh,
b2=6-nf-1/2nh,
b3=9-nf, where nf is the
number of quarks (in the Standard Model) and nh the
number of Higgs doublets. (In the MSSM one has two Higgs
doublets!) Compute the LL solution for the running couplings
above MSUSY taking the values at MZ as
an input. (Note that this can be done in very compact form.)
Can you find scales MSUSY and MGUT
such that unification is realized at the scale
MGUT? Note that you should account for the fact that
the low energy data for the couplings have experimental
uncertainties. Is the SUSY SU(5) unification scenario consistent
with low energy data? Which scales for MSUSY are
the ones most favored by the analysis?
- (c) Think about the conditions that needed to be satisfied to make
the LL analysis carried out above valid. What does the analysis
tell you? Discuss the physical implications.
Maximal Syllabus (we will not cover all of the items)
- Introductory Part
- Review of the Standard Model
- Standard Model as part of an effective theory.
- Renormalization and Loops, Part I
- Decoupling,
- EFT for QED with massive fermions,
- EFT for the Standard Model for heavy top, W, Z
- Unification of gauge couplings
- Renormalization and Loops, Part II (mixing)
- General Aspects of QCD
- Behavior of High-Order Perturbation Theory
- Power Corrections
- Renormalons
- Heavy-Quark-Effective Theory
- Symmetries, Action, Power Counting
- Form Factors, CKM Matrix Elements
- Radiative Corrections, Renormalization
- Non-perturbative Corrections
- Inclusive, Semileptonic Decays
- Non-relativistic QCD
- Degrees of Freedom, Action, Velocity Power Counting
- Derivation of the Nonrelativistic Schroedinger Equation
- Lamb-Shift
- Chiral Perturbation Theory
- Chiral Symmetry, Anomalies, Power Counting
- Electromagnetic Processes
- Pion, Kaon Processes
- QCD Factorization, Soft Collinear Effective Theory
- Collinear Fields and Operators, Symmetries, Power Counting
- Factorization
- Deep Inelastic Scattering
- B Decays into light Hadrons
- Aspects of Jet Physics
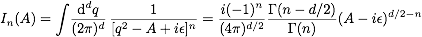 in d=4-2ε dimensions, where A is a real number. We assume
that there are one time and d-1 spatial dimensions. You
are supposed to do the computation in two different ways. Use
Mathematica or tables when needed.
in d=4-2ε dimensions, where A is a real number. We assume
that there are one time and d-1 spatial dimensions. You
are supposed to do the computation in two different ways. Use
Mathematica or tables when needed.
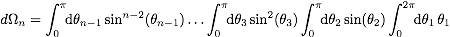 and has the result
and has the result
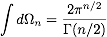 .
.  .
Convince yourself that it is UV and IR divergent for
d=4. Idenfify the UV-divergence by making the massless
propagators massive,
q2+iε→
q2-m2+iε. Determine the form of the
IR divergence for ε→ 0. Use Mathematica to expand
the d-dimensional result for small ε.
.
Convince yourself that it is UV and IR divergent for
d=4. Idenfify the UV-divergence by making the massless
propagators massive,
q2+iε→
q2-m2+iε. Determine the form of the
IR divergence for ε→ 0. Use Mathematica to expand
the d-dimensional result for small ε.
 and
and
 .
The first relation is used when A and B have the same mass
dimensions and x is dimensionless. The second relation is used
then A and B have different dimensions, and [λ]=[B]-[A].
.
The first relation is used when A and B have the same mass
dimensions and x is dimensionless. The second relation is used
then A and B have different dimensions, and [λ]=[B]-[A].
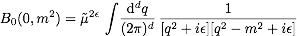 in
two ways. (The term
in
two ways. (The term
 is just a constant.)
is just a constant.)
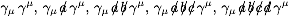 and
the traces
and
the traces
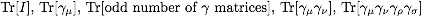 in
4 and d dimensions.
in
4 and d dimensions.
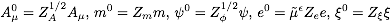 between bare and renormalized fields, mass and coupling. Use that
to one-loop order one can expand the renormalization constants as
between bare and renormalized fields, mass and coupling. Use that
to one-loop order one can expand the renormalization constants as
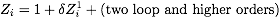 .
.
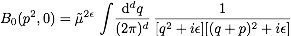 that was
used in class for the renormalization of the photon 2-point function.
that was
used in class for the renormalization of the photon 2-point function.
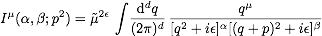 and
and
 .
.
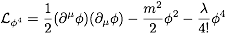 .
Proceed as was done in class for QED.
In this exercise you need to apply most of what you have learned
before. Do the simplest possible computations to get the results
particularly for the 4-point functions. The results are relevant
for the Higgs sector of the Standard Model.
.
Proceed as was done in class for QED.
In this exercise you need to apply most of what you have learned
before. Do the simplest possible computations to get the results
particularly for the 4-point functions. The results are relevant
for the Higgs sector of the Standard Model.
 and
compute the vacuum expectation value v. Show that the scalar field
has the mass
and
compute the vacuum expectation value v. Show that the scalar field
has the mass
 .
Now assume that φ4-theory is a model for the
Standard Model Higgs. This model is actually quite accurate in
many respects.
We know that
.
Now assume that φ4-theory is a model for the
Standard Model Higgs. This model is actually quite accurate in
many respects.
We know that
 and
can use the MS
and
can use the MS
 in the Higgs mass expression.
Determine the renormalization scale μ where the Higgs self
coupling diverges and the theory for sure breaks down as a
function of the Higgs mass. Which field theoretic and physical
conclusions do you have to draw? Why - in this light - is LHC a
no-loose experiment?
in the Higgs mass expression.
Determine the renormalization scale μ where the Higgs self
coupling diverges and the theory for sure breaks down as a
function of the Higgs mass. Which field theoretic and physical
conclusions do you have to draw? Why - in this light - is LHC a
no-loose experiment?
 for the QED coupling renormalization constant and determine the
two-loop renormalization group equation pushing the computation
we did in class to one higher order. Show that, if the
renormalization group equation is finite for
for the QED coupling renormalization constant and determine the
two-loop renormalization group equation pushing the computation
we did in class to one higher order. Show that, if the
renormalization group equation is finite for
 ,
b is not independent but a function of a. Determine the function.
,
b is not independent but a function of a. Determine the function.
 .
You can think of this integral as being a simplified version of a loop-Feynman
diagram where the denominator corresponds to a propagator structure. The
concepts discussed in this exercise apply to usual Feynman diagrams as well.
It is your task to compute the expansion for small a<<1. Naive expansion
in a before integration does not work because of an IR singularity.
You might want to compute the integral exactly and then expand the result
for small a, but this is very difficult. Instead use the two methods
below. Use Mathematica for the computations so same some work.
.
You can think of this integral as being a simplified version of a loop-Feynman
diagram where the denominator corresponds to a propagator structure. The
concepts discussed in this exercise apply to usual Feynman diagrams as well.
It is your task to compute the expansion for small a<<1. Naive expansion
in a before integration does not work because of an IR singularity.
You might want to compute the integral exactly and then expand the result
for small a, but this is very difficult. Instead use the two methods
below. Use Mathematica for the computations so same some work.
 .
where
.
where
 is the D-dimensional
angular integral and
is the D-dimensional
angular integral and
 .
.
